Math Portfolio
Here is a place where I would like to display to you a collection of work that took place during my math methods class, focusing specifically on the work that took place from an instructional book called Baker's Choice by Dan Fendel and Diane Resek with Lynne Alper and Sherry Fraser.
This unit of work focused on demonstrating an Interactive Mathematics Program (IMP). In this unit, rather than having an array of traditional problems that allow the mathematician to repeat the use of a skill in order to acquire it, the unit highlighted a few real life word problems that were discussed and processed in layers, in order to develop skills and understanding related to linear programming problems. The main problem, after which the book is named, is Baker's Choice. This problem involved two people, named The Woo's, who own a bakery and are deciding what kind of cookies to make in order to maximize the profits. The Woo's have to consider various constraints in order to make their decision, such as limited time, oven space, dough, icing, and costs. Not only that, but they may be able to make cookies that are iced and cookies that are not iced, that sell at different prices and cost different amounts of money to make. How will the Woo's maximize their profit?
To the untrained student, this problem threatens to overwhelm and discourage. However, after experiencing this unit I can claim that Baker's Choice is prepared to help any student understand and tackle such a problem using IMP methods. This complex problem is broken apart into components that allows the student to view all the possible solutions of one constraint at a time, such as availability of dough. The student is able to make a decisions about maximizing profits just based on the one constraint. Later, additional constraints may be considered in order to encourage and challenge the students thinking. This broken down method provides a very fluid and intuitive learning environment. The acquisition of the skills required to solve a linear programming problem such as this occurs without the student even realizing that is what they are doing. By the end, the student is able to complete other linear programming problems, without ever even hearing the term used in class. I was able to provide steps to solve the problem, examples of how to do it, and replicate the process without ever considering the classification of the type of problem I was doing.
Sprinkled in with this Baker's Choice problem, are a number of seemingly unrelated word problems that act as a preparation for tackling each of the mathematical concepts required for solving linear programming problems. These problems are called POWs, or Problems of the Week, and are worked on throughout the week by the student at home. In class time, as the student is mulling over the issues confronted with a POW in the background of their mind, they are tackling Baker's Choice in the forefront of their mind. These POWs serve as a powerful force on the direction of the mind while working on Baker's Choice in class, or the other linear programming problems that are later introduced. At first, it feels like some kind of Jedi Mind Trick, but as I continued to experience the unit I could see my abilities and understanding grow.
This unit of work focused on demonstrating an Interactive Mathematics Program (IMP). In this unit, rather than having an array of traditional problems that allow the mathematician to repeat the use of a skill in order to acquire it, the unit highlighted a few real life word problems that were discussed and processed in layers, in order to develop skills and understanding related to linear programming problems. The main problem, after which the book is named, is Baker's Choice. This problem involved two people, named The Woo's, who own a bakery and are deciding what kind of cookies to make in order to maximize the profits. The Woo's have to consider various constraints in order to make their decision, such as limited time, oven space, dough, icing, and costs. Not only that, but they may be able to make cookies that are iced and cookies that are not iced, that sell at different prices and cost different amounts of money to make. How will the Woo's maximize their profit?
To the untrained student, this problem threatens to overwhelm and discourage. However, after experiencing this unit I can claim that Baker's Choice is prepared to help any student understand and tackle such a problem using IMP methods. This complex problem is broken apart into components that allows the student to view all the possible solutions of one constraint at a time, such as availability of dough. The student is able to make a decisions about maximizing profits just based on the one constraint. Later, additional constraints may be considered in order to encourage and challenge the students thinking. This broken down method provides a very fluid and intuitive learning environment. The acquisition of the skills required to solve a linear programming problem such as this occurs without the student even realizing that is what they are doing. By the end, the student is able to complete other linear programming problems, without ever even hearing the term used in class. I was able to provide steps to solve the problem, examples of how to do it, and replicate the process without ever considering the classification of the type of problem I was doing.
Sprinkled in with this Baker's Choice problem, are a number of seemingly unrelated word problems that act as a preparation for tackling each of the mathematical concepts required for solving linear programming problems. These problems are called POWs, or Problems of the Week, and are worked on throughout the week by the student at home. In class time, as the student is mulling over the issues confronted with a POW in the background of their mind, they are tackling Baker's Choice in the forefront of their mind. These POWs serve as a powerful force on the direction of the mind while working on Baker's Choice in class, or the other linear programming problems that are later introduced. At first, it feels like some kind of Jedi Mind Trick, but as I continued to experience the unit I could see my abilities and understanding grow.
Math Work
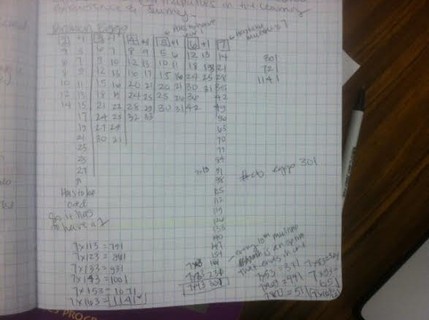
Broken Eggs
This POW was performed in the beginning of the semester. This helped me recognize numerical patterns that I could use to make rules and conjectures. This problem asked for one number that was evenly divided by 7, but also divisible by 2, 3, 4, 5, and 6 with a remainder of 1. You can see where I started making lists of similar numbers, but then after a while I noticed a pattern and started making rules of what I thought would be true. I started to simplify my process using these rules and narrowed down my search until I found a number that fit the constraints.
This POW was performed in the beginning of the semester. This helped me recognize numerical patterns that I could use to make rules and conjectures. This problem asked for one number that was evenly divided by 7, but also divisible by 2, 3, 4, 5, and 6 with a remainder of 1. You can see where I started making lists of similar numbers, but then after a while I noticed a pattern and started making rules of what I thought would be true. I started to simplify my process using these rules and narrowed down my search until I found a number that fit the constraints.

Kick It!
This POW was done about half way through the unit. It helped me realize the usefulness of setting variables and creating equations in order to express constraints. This problem introduce a football game that had different rules for scoring. It asked for scores that would be impossible based on the scoring that was outlined. From the top of the page I defined the rules for field goals and touch downs, as well as the impossible solutions that were provided in the problem. I then started to define possible numbers, which seemed to lead me no where. Eventually, I got to the point where I created a formula using the scoring information in order help me narrow down possible solutions. I was able to use my knowledge from the Broken Eggs problem, and take it a step further.
This POW was done about half way through the unit. It helped me realize the usefulness of setting variables and creating equations in order to express constraints. This problem introduce a football game that had different rules for scoring. It asked for scores that would be impossible based on the scoring that was outlined. From the top of the page I defined the rules for field goals and touch downs, as well as the impossible solutions that were provided in the problem. I then started to define possible numbers, which seemed to lead me no where. Eventually, I got to the point where I created a formula using the scoring information in order help me narrow down possible solutions. I was able to use my knowledge from the Broken Eggs problem, and take it a step further.

Big State U
This problem is a linear programming problem where I realized that I was able to complete the entire task, considering all constraints on my own. The problem presented an admission situation where only a certain number of students with certain criteria could be admitted to the college. I broke apart the constraints in their own separate sections with their own graphs. I jumped passed the steps I used in Broken Eggs and Kick It, and went straight to defining variables and expressing constraints in an equation. Then I decided to represent it by graphing a feasible region. I compared each of these graphs together in order to come up with the most reasonable solution.
This problem is a linear programming problem where I realized that I was able to complete the entire task, considering all constraints on my own. The problem presented an admission situation where only a certain number of students with certain criteria could be admitted to the college. I broke apart the constraints in their own separate sections with their own graphs. I jumped passed the steps I used in Broken Eggs and Kick It, and went straight to defining variables and expressing constraints in an equation. Then I decided to represent it by graphing a feasible region. I compared each of these graphs together in order to come up with the most reasonable solution.
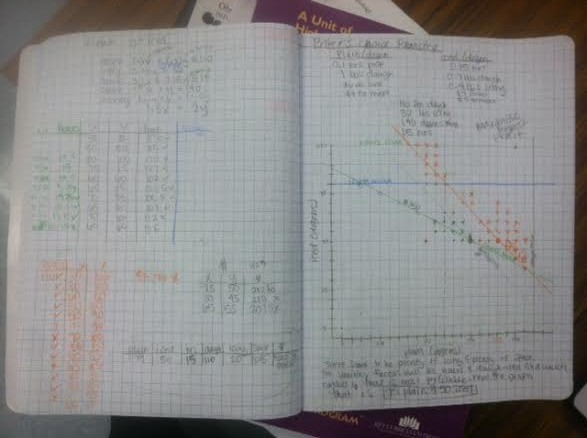
Baker's Choice
Here I wanted to display the final Baker's Choice conquest, where I took on the problem in its entirety at the end of the unit. I graphed all constraints on one graph in different colors. All steps of the processed occurred fluidly and intuitively. I was able to consider all constraints and give a reasonable and arguable solution.
Here I wanted to display the final Baker's Choice conquest, where I took on the problem in its entirety at the end of the unit. I graphed all constraints on one graph in different colors. All steps of the processed occurred fluidly and intuitively. I was able to consider all constraints and give a reasonable and arguable solution.
This class has been a wonderfully eye opening experience about teaching and especially about math. I hope you enjoyed the work as much as I did.
Statement of Personal Growth
When I first started this class, I was probably more closed off to group work than I would like to admit. I had my mind focused on what would be required of me in order to pass the class. From the first day I felt challenged by open ended questions and discussions. It felt bizarre to have the teacher "go with" whatever students said in class by said things like "That's interesting that you interpreted the question that way". All interpretations were accepted and invited, and it felt weird. As the class progressed I felt excited and invigorated by the idea that I could explore and be creative, without the pressure of delivering a wrong answer. It was liberating that there was no one right way to interpret the questions that were asked. I felt empowered to explore and see math anew. I had experienced math before, but never in this way.
I came into class with a significant understanding of many mathematical concepts, and even though my high school curriculum of mathematics was different than most, I have experienced the traditional classroom with "drill and kill" mentality of teaching. Practice makes perfect. Luckily for me, I tend to have a logical and systematic way of thinking that suited me well for understanding math even in the most unlikely of circumstances. However, after engaging in math in this IMP fashion, I was learning new things about it that I had never conceived before.
I saw that you don't need to practice to make perfect. By using the IMP methods, you have one very well designed word problem with many layers, that is expounded upon by asking a very well placed question. I realized the importance of doing the work on my own first in order to wrap my brain around the problem, before I can discuss it, or even understand another's point of view about it. It surprised me to learn that I do in fact enjoy group work. The discussions that were had propelled my thinking beyond what I could do on my own, leading me to look forward to hear what others would say and come up with. I realized for the first time that math is creative, and that its unique to each person. I see the value in changing what my preconceived ideas about math was, and that incorporating the key elements of a program like IMP into a curriculum is valuable. After having experienced my it myself, I see that at this time in education, I see that it is very much needed for the excellence of student education.
Statement of Personal Growth
When I first started this class, I was probably more closed off to group work than I would like to admit. I had my mind focused on what would be required of me in order to pass the class. From the first day I felt challenged by open ended questions and discussions. It felt bizarre to have the teacher "go with" whatever students said in class by said things like "That's interesting that you interpreted the question that way". All interpretations were accepted and invited, and it felt weird. As the class progressed I felt excited and invigorated by the idea that I could explore and be creative, without the pressure of delivering a wrong answer. It was liberating that there was no one right way to interpret the questions that were asked. I felt empowered to explore and see math anew. I had experienced math before, but never in this way.
I came into class with a significant understanding of many mathematical concepts, and even though my high school curriculum of mathematics was different than most, I have experienced the traditional classroom with "drill and kill" mentality of teaching. Practice makes perfect. Luckily for me, I tend to have a logical and systematic way of thinking that suited me well for understanding math even in the most unlikely of circumstances. However, after engaging in math in this IMP fashion, I was learning new things about it that I had never conceived before.
I saw that you don't need to practice to make perfect. By using the IMP methods, you have one very well designed word problem with many layers, that is expounded upon by asking a very well placed question. I realized the importance of doing the work on my own first in order to wrap my brain around the problem, before I can discuss it, or even understand another's point of view about it. It surprised me to learn that I do in fact enjoy group work. The discussions that were had propelled my thinking beyond what I could do on my own, leading me to look forward to hear what others would say and come up with. I realized for the first time that math is creative, and that its unique to each person. I see the value in changing what my preconceived ideas about math was, and that incorporating the key elements of a program like IMP into a curriculum is valuable. After having experienced my it myself, I see that at this time in education, I see that it is very much needed for the excellence of student education.